What types of triangles are there?
A triangle is the simplest polygon. That is, a flat geometric figure that consists of three edges and three vertices, which add up to 180º. Types of triangles are classified according to their characteristics. That is, according to the size of their edges and angles.
Types of Triangles according to their edges

The names of the triangles according to their edges are: equilateral, isosceles and scalene. Each of them has different characteristics that we will elaborate on below.
Equilateral triangle
The equilateral triangle is one that is characterized by having three equal sides. Consequently, all the angles of an equilateral triangle are 60º. The equilateral triangle is a regular polygon.
Isosceles triangle
Isosceles triangles are characterized by having two equal sides and one that is different. Consequently, it also has two equal angles.
Scalene triangle
A scalene triangle is one that is characterized by having all its sides and angles unequal. That is, different from each other in length and degrees, respectively.
Types of Triangles according to their angles
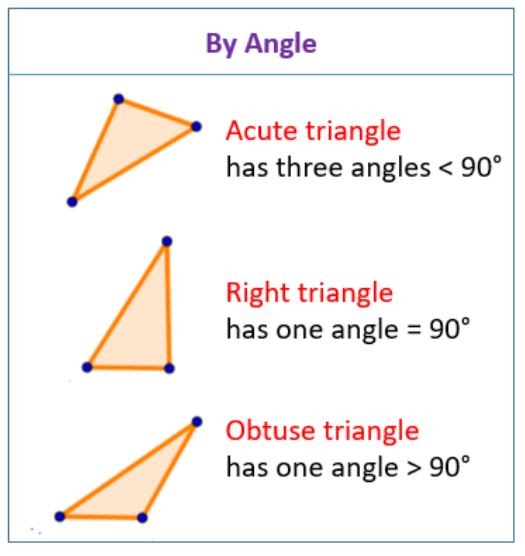
Triangles can be classified according to the size of their angles. Angles can be straight (equal to 90º), acute (less than 90º) and obtuse (greater than 90º).
Right triangle
Right triangles are those that are formed by a straight angle and two acute angles. Therefore, the long side is the hypotenuse.
For example, isosceles and scalene triangles, can also be classified as right triangles. This, however, can never be the case with an equilateral triangle since the measure of its angles is invariable.
Oblique triangle
Oblique triangles are those that are characterized by not having any right angles. In this group are both acute and obtuse angles that, although they are different from each other, share this characteristic.
- Acute triangles: have three acute angles.
- Obtuse triangles: have one obtuse angle and two acute angles.
RELATED POSTS:

1 Comment
nice and great for my child!